Fractales famosos

En los fractales, lo que se trata es de mirar con más detenimiento y alcanzar a ver algo más. Ellos tienen mucho que ver con la maravillosa atracción de la Naturaleza en cualquier escala: desde las estructuras microscópicas hasta las incontables galaxias. Veamos entonces cómo apreciar más de cerca estas maravillas, a partir de dos fractales muy famosos: el conjunto de Mandelbrot, y el triángulo de Sierpinsky.

El conjunto de Mandelbrot

Es una estructura matemática de fascinante belleza obtenido con un algoritmo de tiempo de escape, de gran valor estético generado por una transformación en el plano complejo tan simple como:

El conjunto de Mandelbrot es una colección de puntos que se encuentran en el plano complejo. Aplicando iterativamente la fórmula anterior a partir de un punto inicial z₀ se tiene la sucesión

que se denomina órbita de z₀ . Si llega a suceder que z_k = z₀ , con z_i ≠ z₀ para

La secuencia se genera a partir de z₀ = 0 + 0i (que es el único crítico de z²+c) y si la órbita permanece acotada, el punto se halla entonces en el conjunto de Mandelbrot.

La siguiente tabla muestra la órbita de este punto, junto con la distancia al origen de cada miembro de la secuencia:

Complejo	Distancia
z₀= 0.000 + 0.000i	ï z₀ ï= 0.000
z₁= 0.370 + 0.400i	ï z₁ ï= 0.545
z₂= 0.347 + 0.696i	ï z₂ ï= 0.778
z₃= 0.006 + 0.883i	ï z₃ ï= 0.883
z₄= -0.409 + 0.410i	ï z₄ ï= 0.580
z₅= 0.369 + 0.064i	ï z₅ ï= 0.375
z₆= 0.502 + 0.447i	ï z₆ ï= 0.672
z₇= 0.422 + 0.849i	ï z₇ ï= 0.948
z₈= -0.173 + 1.117i	ï z₈ ï= 1.130
z₉= -0.848 + 0.014i	ï z₉ ï= 0.848
z₁₀= 1.089 + 0.376i	ï z₁₀ ï= 1.152
z₁₁= 1.415 + 1.219i	ï z₁₁ï= 1.868
z₁₂= 0.885 + 3.850i	ï z₁₂ ï= 3.950

Observamos que la órbita comienza escapando hacia fuera y después regresa a un valor mínimo en z₅ , para comenzar de nuevo a girar en redondo hacia el exterior. El valor de z₁₂ es el primero en escapar de un círculo de radio 2. Esto demuestra que el punto 0,37+0.4i no se encuentra en el conjunto de Mandelbrot.

Complejo	Distancia
z₀= 0.000 + 0.000i	ï z₀ ï= 0.000
z₁= 0.370 + 0.200i	ï z₁ ï= 0.421
z₂= 0.467 + 0.348i	ï z₂ ï= 0.582
z₃= 0.467 + 0.525i	ï z₃ ï= 0.703
z₄= 0.312 + 0.690i	ï z₄ ï= 0.758
z₅= -0.009 + 0.631i	ï z₅ ï= 0.631
...	...
z₉₆= 0.352 + 0.479i	ï z₉₆ ï= 0.594
z₉₇= 0.264 + 0.537 i	ï z₉₇ ï= 0.598
z₉₈= 0.152 + 0.484i	ï z₉₈ ï= 0.507
z₉₉= 0.159 + 0.347i	ï z₉₉ ï= 0.382
z₁₀₀= 0.275 + 0.310i	ï z₁₀₀ï= 0.415

Para los primeros 100 valores vemos que la secuencia de las órbitas se encuentran dentro del círculo de radio 2

Esta órbita parece ser, muy convincentemente, una órbita que no escapa al infinito, pero eso no quiere decir que no puedan escapar valores posteriores. El conjunto de Mandelbrot debe aproximarse definiendo un punto límite arbitrario para cuantos valores de la órbita vayan a ser probados. Diremos que el punto 0.37+0.2i se encuentra dentro del conjunto porque los N valores que se probaron se encontraban dentro del círculo de prueba.

El conjunto así generado está formado por una cardioide principal. La parte circular adyacente es un círculo con centro en ( -1 ; 0 ) y radio 1/4. Sobre el eje x el fractal de Mandelbrot muestra comportamiento de bifurcación para los valores x = -3/4, -5/4, -1,3681, -1,3940, ...

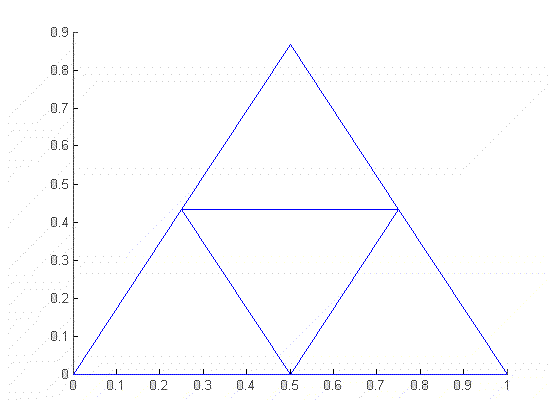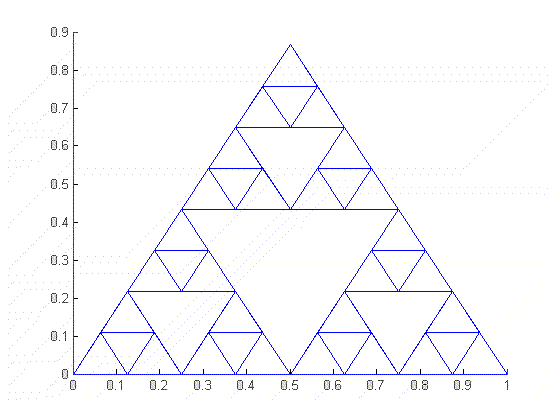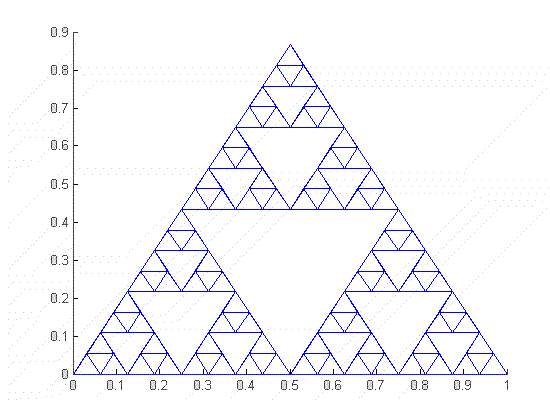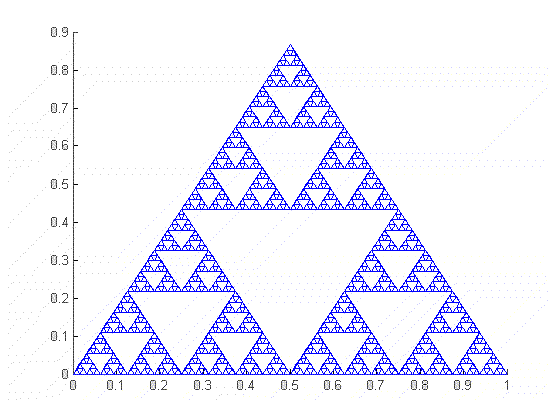
El triángulo de Sierpinsky

El triángulo de Sierpinsky puede especificarse con exactitud estableciendo la norma que determina su autosimilaridad: es un objeto generado a partir de un triángulo. A partir de los puntos medios de los lados se construyen nuevos triángulos; en cada paso, el triángulo central es retirado como puede observarse en la figura, de forma que los nuevos triángulos son una réplica autosemejante exacta del original: