Propiedades de los fractales
Clasificación
Los fractales pueden ser físicos o matemáticos, según sean el producto de la naturaleza o la tecnología, o de la abstracción. Una propiedad característica de cualquier curva o superficie fractal es su autosimilaridad o autosemejanza, la cual consiste en que una porción cualquiera de la curva o superficie es similar al todo. Los fractales matemáticos se construyen de manera tal que satisfacen exactamente el criterio de autosemejanza.

Las propiedades de los fractales incluyen independencia de escala, autosimilaridad, complejidad y perímetro infinito. En el análisis fractal el concepto de “longitud” se caracteriza con un parámetro D denominado dimensión fractal, el cual puede dar una medida de la complejidad de la estructura. Sin embargo, las condiciones necesarias y suficientes para que un objeto posea propiedades fractales no han sido formalmente definidas, a pesar de lo cual este tipo de geometría permite describir la irregularidad inherente de muchas estructuras presentes en la naturaleza, como las obtenidas en procesos de cristalización, los crecimientos que se observan cuando se inyecta un fluido en otro más viscoso y la electrodeposición de metal sobre un electrodo. En la figura se presenta un ejemplo de patrones de crecimiento típicos en cristales.

Dimensión fractal
Formalmente, un fractal matemático se define como una serie para la cual la
dimensión de Hausdorff-Besicovitch excede su dimensión topológica discreta
[2]. Una dimensión fractal cuantifica el grado en el cual un objeto “llena”
el espacio donde yace. Por ejemplo, para 1 < D < 2, cuantifica el grado en
el cual un trazo llena el plano. Ya a finales del siglo XIX se había
descubierto que algunos conjuntos de puntos tenían dimensión fraccionaria.
Surgió entonces la necesidad de redefinir el concepto de dimensión, de tal
manera que las líneas, las superficies y los sólidos siguieran siendo uni, bi
y tridimensionales y que se les pudiera asignar dimensión a las nuevas
estructuras.
El meteorólogo inglés Lewis Fry Richardson (1881-1953) fue el primero en
tropezar con estos inconvenientes al querer medir la costa oeste de Gran Bretaña:
se observó que había una fuerte variación en los resultados según la escala
usada.
No resulta difícil averiguar dónde radica la dificultad. La costa de Bretaña
es muy irregular por encontrarse llena de accidentes geográficos de gran
complejidad. Un instrumento de medida bastante largo no se dobla con tantos
recodos y curvas; un instrumento de medida más pequeño se ajusta mejor al
contorno, aumentando de este modo los valores obtenidos, llegando por este
camino a obtener una longitud que se extiende en el límite al infinito.
Aparentemente, sería mas útil no hablar de la longitud de la costa, sino
especificar su grado de sinuosidad numéricamente.
Cuando una bahía o una península representadas en un mapa a escala
1/100000 se observa en una escala 1/10000 aparecen nuevas bahías y penínsulas.
Este proceso podría repetirse indefinidamente y los distintos mapas seguirían
evidenciando los mismos rasgos genéricos, es decir, cada parte de la costa es
homotética al todo.
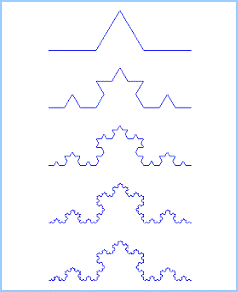
Un modelo muy simplificado de una costa que permite describir este fenómeno
es la construcción de la curva de Von Koch. Ésta parte de un segmento de
longitud 1. El tercio central se reemplaza por otros dos segmentos de igual
longitud al eliminado. La figura así obtenida tiene perímetro 4X1/3 = 4/3. Se
hace lo mismo con cada uno de los 4 lados y así sucesivamente, obteniéndose lo
que se observa en la figura.
Las longitudes de las aproximaciones sucesivas de la curva de Von Koch y de otras curvas similares no son magnitudes que deban estimarse empíricamente, sino que pueden ser calculadas exactamente: el procedimiento se basa en la propiedad elemental que caracteriza el concepto de dimensión euclídea de los elementos geométricos sencillos que poseen homotecia interna. La noción de autosemejanza se vincula con el concepto intuitivo de dimensión. Un segmento puede dividirse en N partes iguales, cada una de las cuales está en relación r =1/N con el segmento total [3]. De igual forma, al dividir un cuadrado en el plano en N partes iguales, se tiene la relación r =1/N1/2 con respecto a la figura completa; en el caso del cubo es r = 1/N1/3 y r =1/N1/D para un objeto D-dimensional.
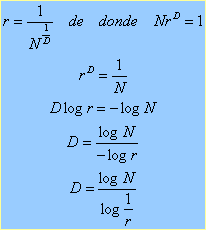
Esta expresión de dimensión tiene significado formal para toda figura que, como la curva de Von Koch, cumple que el todo se puede descomponer en N partes que se pueden deducir de él por una homotecia de razón r. El D así obtenido no tiene por qué ser entero. Por ejemplo, en el caso de la curva de Von Koch, N = 4 y r =1/3, con lo que D= log 4/log 3 (aprox.1,26).